=> Liste der Artikel <=
 Détails sur le calcul de puissance de Quintana au Mont Ventoux, par Frédéric Portoleau
Détails sur le calcul de puissance de Quintana au Mont Ventoux, par Frédéric Portoleau
26-03-2020, 10:42 - Frédérc Portoleau
Cet article est un complément de l'article du mois dernier traitant des performances récentes de Quintana.
Le modèle de calcul de puissance d'un cycliste, de James Martin, est utilisé à vitesse constante (ref 1 ou ici). Une correction est ajoutée pour tenir compte du drafting.
Le tableau suivant décrit les paramètres de la modélisation:
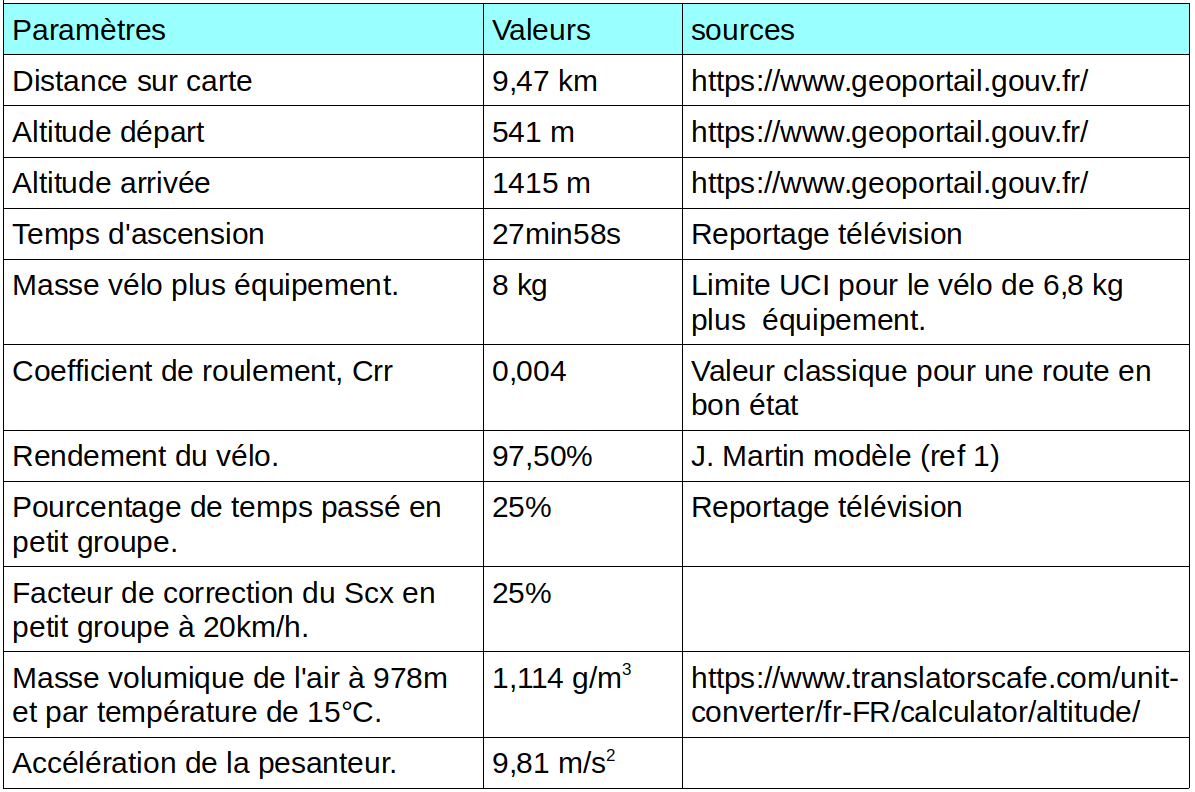
La distance mesurée sur la carte fournit la distance horizontale. Une petite correction en fonction de la pente doit être appliquée pour obtenir la distance réellement parcourue, soit 9,52 km. La vitesse moyenne est alors de 20,42 km/h, soit 5,67 m/s. La pente moyenne est de 9,18%.
Drafting:
Il y a peu d'études disponibles sur l'effet de drafting à faible vitesse, à moins de 25 km/h. L'essentiel des publications concernent des études où les vitesses sont supérieures à 40 km/h comme la poursuite par équipe sur vélodrome couvert.
La position sur le vélo, l'équipement, l'emplacement dans le peloton, le nombre de rangées de coureurs, la distance entre les coureurs, la taille du coureur juste devant, le vent peuvent influencer de manière significative les économies de traînée aérodynamique réelles d'un coureur roulant en groupe (ref 2/ici, et ref 3/ici). La présence des motos devant ou à côté des coureurs est aussi un paramètre à ne pas négliger (ref 5/ici). Dans le meilleur des cas, coureur en position optimale, la réduction du Scx approcherait les 50% en cyclisme sur piste pour une poursuite à 4 coureurs. Pour un contre la montre par équipe de 9 coureurs sur route, la réduction de Scx pourrait atteindre 60% pour les coureurs en position 5 à 8, bien alignés et avec un espacement de 0,05m (ref 6/ici). Au coeur d'un peloton idéal de forme constante et optimal de 121 coureurs bien en ligne, la réduction de Scx pourrait être de 90% pour certains emplacements (ref 4/ici). Le vent latéral a tendance à réduire l'effet du drafting. Par exemple avec un vent latéral de 5°, la réduction de Scx passerait de 41% à 30% d'après une étude (ref 7/ici) sur un coureur abrité à 20cm en position haute, les mains sur le guidon.
La distance latérale, sur une seule ligne, entre coureurs joue aussi un rôle. En peloton réel, les espaces entre coureurs et la largeur des routes varient. Il y a également des virages et des variations de vitesse, la réduction de Scx est donc inférieure aux cas théoriques évoqués ci dessus. En montée de col, la puissance pour vaincre la pesanteur est prédominante.
Le point important est de réaliser des estimations de puissance quand la pente est forte (plus de 7 %), le vent faible, à vitesse réduite (moins de 25km/h) quand les forces aérodynamiques n'ont pas trop d'influence. La détermination du drafting réel est impossible avec précision. J'ai fait le choix, en attendant de nouvelles études, d'appliquer une réduction de 30% si un peloton contient plusieurs lignes et de 25% si il y a une seule ligne de coureurs.
Estimation de la puissance réelle développée par Nairo Quintana :

Le vent est supposé être nul (voir article précédent). Le Scx est corrigé en tenant compte du pourcentage de temps passé en petit groupe, soit Scx=0,309 m2 (75% du temps avec un Scx de 0,33 et 25% du temps avec un Scx de 0,33*0,75).
Puissance pour vaincre la pesanteur : Ppes=(57+8)*9,81*5,67*0,0918 = 332 watts
Puissance pour vaincre les frottements de l'air : Pair=1/2*1,114*0,309*(5,67)3 = 31 watts
Puissance pour vaincre les frottements de roulement : Pr=(57+8)*9,81*5,67*0,004 = 15 watts
Puissance totale = (332 + 31 + 15) / 0,975 = 388 watts soit 6,8 w/kg
Si une masse corporelle de 59 kg est utilisée, la puissance externe estimée de Nairo Quintana est alors de 399 watts soit 6,75 w/kg
Incertitudes de l'estimation de la puissance absolue : 4% = 15 watts.
L'incertitude mathématique est calculée avec la méthode décrite dans un précédent article.
Les Incertitudes de chaque paramètre sont les suivantes :
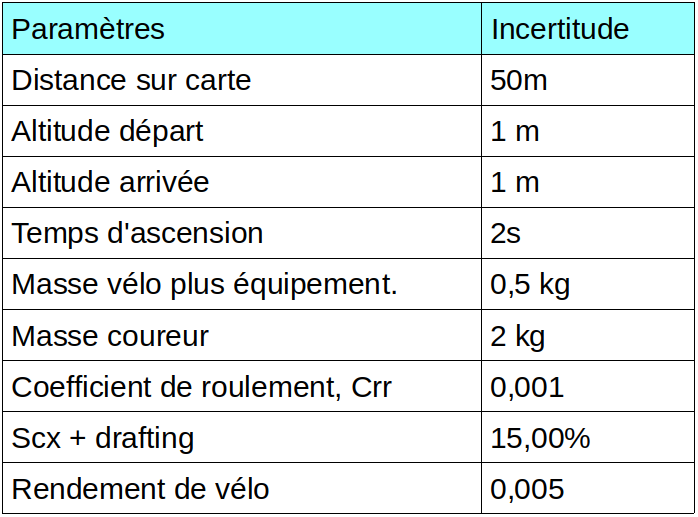
Estimation de la puissance étalon 78 kg avec vélo :

Puissance pour vaincre la pesanteur : Ppes=(70+8)*9,81*5,67*0,0918 = 399 watts
Puissance pour vaincre les frottements de l'air : Pair=1/2*1,114*0,348*(5,67)3 = 35 watts
Puissance pour vaincre les frottements de roulement : Pr=(70+8)*9,81*5,67*0,004 = 17,5 watts
Puissance totale = (399 + 35 + 17,5) / 0,975 = 463 watts soit 6,6 w/kg
Incertitudes de l'estimation de la puissance étalon absolue : 2,3 % = 11 watts
Frédéric Portoleau
References :
[1]
Validation of a Mathematical Model for Road Cycling Power
https://www.researchgate.net/publication/279937184_Validation_of_a_Mathematical_Model_for_Road_Cycling_Power
[2]
The impact of relative athlete characteristics on the drag reductions caused by drafting when cycling in a velodrome.
https://journals.sagepub.com/doi/full/10.1177/1754337117692280
[3]
Aerodynamic drag in cycling pelotons: New insights by CFD simulation and wind tunnel testing.
https://www.sciencedirect.com/science/article/pii/S0167610518303751
[4]
CFD simulations of the aerodynamic drag of two drafting cyclists.
http://www.urbanphysics.net/2013_CAF_BB_TD_EK_JC_PH__Preprint.pdf
[5]
Aerodynamic benefit for a cyclist by a following motorcycle
https://www.sciencedirect.com/science/article/pii/S0167610516302306
[6]
Aerodynamic drag in cycling team time trials
https://www.sciencedirect.com/science/article/pii/S0167610518306755
[7]
Drafting Effect in Cycling: Investigation by Wind Tunnel Tests
https://www.sciencedirect.com/science/article/pii/S1877705816306336







